Probability and Distributions

 

 

안녕하세요! 제이덥입니다~ 이글은 Mathematics for Machine Learning 의 Chapter 6의 번역글입니다. 제대로 된 번역글이 없어 직접 번역을 하여 작성했으며 의역이 포함되어 있으며 원글은 아래 Reference에서 확인해 주세요~

확률의 개념

확률(probability)를 대략적으로 설명하자면 불확실성(uncertainty)에 대한 연구라고 말할 수 있다. 확률은 또한 사건이 발생할 비율 혹은 사건이 발생할 믿음의 정도라고 볼수도 있다. 이렇게 만들어진 확률을 실험상에서 어떤 일이 발생할 정도를 측정하는데 활용된다.

확률 변수와 확률 분포

확률 변수의 개념

종종 우리는 데이터, 기계 학습 모델, 모델의 예측값들의 불확실성(uncertainty)을 정량화한다. 이 불확실성을 정량화하는 작업은 확률변수(random variable)를 필요로 한다. 확률변수(Random Variable)란 임의의 실험에 대한 결과와 우리가 관심있는 특성들의 집합을 맵핑(mapping)해주는 일종의 함수이다.

확률 분포

확률 변수를 이용해서 특정한 결과값이 일어날 확률을 측정하는것을 확률 분포(Probability)라고 부른다.

확률 분포는 아래와 같이 다른 개념을 이해하기 위한 하위 개념으로 활용된다.

• 8.4 확률적 모델링(probabilistic modeling)
• 8.5 그래프 모형(graphical models)
• 8.6 모형 선택(model selection)

다음장부터 확률 공간(probabilty space)를 정의하기 위한 표본 공간(the sample space), 사상(event), 사상의 확률(probability of an event)등 세가지 개념을 배우며, 해당 개념과 확률 변수와 어떤 관계가 있는지 살펴볼 것이다. 이 6.1 Chapter에서는 타이트하게 개념을 설명하는 것은 개념 넘어에 있는 직관을 방해할 수 있기 때문에 의도적으로 논리적인 단계를 지키지않고 개념을 설명하고 있다. 아래 다이어그램은 이 Chapter6 확률분포에서 배우는 개념들의 관계를 도식화한 것이다.

Construction of Probability Space

확률의 목적

확률에 관한 이론적 목적은 실험의 결과 값들을 설명하기 위해 수학적 구조를 정의하는 것이다.

예로 하나의 코인을 던질 때, 단 한번의 결과를 예측할 수는 없지만 무수히 많은 횟수의 코인을 던진다면 평균적인 결과 값의 규칙성(regularity)를 발견할 수 있다.

 

이러한 수학적인 구조(mathematic structure)를 이용하여 확률의 최종적인 목적은 자동화된 추론(automated resoning)을 하는데 있으며, 이러한 관점에서 확률은 논리적 추론을 일반화한다.(Jaynes 2003)

확률의 철학적 문제

자동화된 추론(automated resoning) 시스템을 구축할 때 전통적으로 사용했던 부울 논리(Boolean Logic)는 플로저블 추론(plausible logic) 형태의 타당성을 제공하지 못한다. 다음의 예시를 살펴보자

 

 

예시 1)

• A,B라는 명제가 있다고 가정하자. A라는 명제가 '거짓'임이 밝혀질 경우, 전통적인 방식의 부울 논리는 B에 대한 어떠한 논리도 제공해주지 않는다. 하지만 일상적인 생활 속에서 해당정보는 B가 덜 그럴듯하다고 판단하게 만들어줄 수 있또한, 다. B라는 명제가 '참'이라고 밝혀질 경우, B가 더 그럴듯해진다고 판단할 수 있다. 우리는 이러한 방식의 논리를 매일 반복적으로 사용한다. 아래의 예시는 조금더 구체적인 상황을 제공한다.
• 조금더 복잡한 경우의 수를 생각해보자. 우리는 친구를 기다리고 있을 때 세가지 상황의 가능성이 있다.
  • H1 : 친구가 제시간에 온다.
  • H2 : 친구가 교통체증으로 인해 늦는다.
  • H3 : 친구가 외계인에게 잡혔다.
    이 상황에서 만일 친구가 늦게 오는 것으로 관찰 될 경우 H1의 가설은 기각된다. H3와 H2의 가설 중 H3는 일반적인 경우에 해당되지 않음으로 H2가 가장 그럴듯한 가설 및 추측이 될 수 있다.

이러한 방식으로 본다면, 확률 이론은 부울 논리의 일반화(Generalization of Boolean Logic)로 여겨질 수 있다. 머신러닝 관점에서, 자동 추론 시스템의 설계를 공식화하기 위해 종종 이러한 방식을 사용하곤 한다. 확률 이론이 어떻게 추론 시스템의 토대가 될 수 있는가에 대한 추가적인 논거는 Pearl (1988)에서 찾을 수 있다.

꾸준하게 확률의 철학적 기반은 연구되어 왔고, E.T. Jaynes(1922–1998)는 다음과 같이 확률이 모두 만족해야하는 세가지 수학적 조건을 제시하였다.

• 1. 신뢰성의 수준은 반드시 실수로 정의된다.
• 2. 실수는 반드시 통상적인 관념에 기반을 두어야한다.
• 3. 추론의 결과는 다음 세가지를 만족하는 일관성(consistency)를 가져야한다.
  • (a) 일관성과 모순없음(consistency and non-contradiction): 모든 경우에 대해 동일한 신뢰성 값을 가져야 한다.
  • (b)정직성(honesty): 모든 데이터를 고려한 결과여야한다.
  • (c) 재현성(Reproduct): 두 문제에 대한 같은 지식을 가지고 있다면, 동일한 수준의 신뢰성에 도달해야한다.

콕스-제인스 정리(The Cox-Jaynes theorem) 정리는 이 기준들이 신뢰성 p부터 단조함수에 이르기까지 수학적 규칙을 설명하기 충분함을 입증한다. 따라서, 이 규칙들은 확률의 규칙이라고 볼 수 있다.

 

참고1.
머신러닝과 기계학습에서는 확률에 대한 두가지의 주요한 해석이 있다.
1. 베이지안 해석(Bayesiam interpretation)(Bishop, 2006)
베이지안 해석에서는 확률을 사용하여 사건에 대한 불확실성을 정한다. "주관적 확률(subjective probability)" 또는 "믿음의 정도(degree of belief)"라고도 불린다.
2.빈도주의 해석(frequent interpretation)(Efron and Hastie, 2016).
빈도주의적 해석에서 발생한 전체 사건 수에 대한 관심 사건의 상대적 빈도를 고려한다. 몇개의 머신러닝의 확률론적 모델에대해 lazy notation과 전문 용어 같이 사용하여 혼란을 주기도 하며, 이 챕터에서도 같은 방식을 선택했다. 여러개의 개면을 모두 "확률 분포"라고 하며, 스스로 의미를 파악해야 한다. 따라서 머신러닝에서 쓰이는 확률 분포를 이해하는데 한가지 팁을 준다면 범주형(이산형 확률 변수) 또는 연속형(연속 확률 변수) 분포인지 구분하여 이해하는 것이다. 해당 개념은 머신러닝에서 매우 주요하게 쓰이는 개념들이기 때문이다.

확률과 확률 변수

확률에 대한 논의에서 앞서 종종 혼동되는 다음 세가지 개념을 확실히 이해하고 있어야한다.

1. 확률 공간(probability space) : 확률을 정량화 할 수 있게 하는 개념. 하지만 이 기본(basic)확률 공간을 사용하여 확률을 다루지 않는다.
2. 확률 변수(random variable) : 확률 변수로 종종 숫자를 이용하여 확률 공간을 접근하며, 확률을 다룰 때 자주 사용한다.
3. 확률 분포(probaility distribution): 확률 변수와 함께 활용하는 개념으으로 6.2 챕터에서 다룰 예정이다.

현대의 확률

현대의 확률은 Kolmogorov(Grinterse and Snell, 1997; Jaynes, 2003)에서 제시하는 아래 세가지 공리에 기반한다.

1. 표본 공간(the sample space)
2. 사건 공간(the event space)
3. 확률 측정(probability measure)

확률 공간은 임의 결과를 갖는 현실 세계(실험)을 모형화한다. 소개할 확률공간은

 

1. 표본 공간(The sample space $\Omega$)

표본 공간은 가능한 모든 실험 결과의 집합이며, $\Omega$로 표기한다. 예를 들어, 두 번의 연속적인 동전던지기는 ${ hh, tt, ht, th}$이다(단, "${h}$"=앞면,"${t}$"=꼬리)
2. 사건 공간(the event space $A$)
사건 공간은 실험의 잠재적 결과의 집합이다. 표본 공간 $\Omega$의 부분집합은 사건 공간 $A$에 포함된다. ($\omega \in \Omega$ 이면 $A$에 속함)따라서 사건 공간 $A$는 표본 공간 $\Omega$의 부분집합을 통해 구할 수 있으며, 이산 확률의 경우 $\Omega$의 멱집합을 통해 구할 수 있다.
3. 확률 $P$(The probability $P$)
($A \in A$)를 만족하는 모든 사건에대해서, $P(A)$ 는 해당 조건이 만족하는 사건이 발생할 정도 혹은 확률을 의미한다. 그리고 $P(A)$ 는 $A$의 확률이라고 말한다.

 

참고2. 표본공간(Sample Space)의 다른 이름
표본 공간(The sample space)은 다른 책에서 다른 이름으로 불리기도 한다. 많이 쓰이는 다른 이름은 "state space"이며 가끔은 동역학계(dynamical system)의 상태를 부르기위해 쓰이기도 한다. 또 다른 이름은 “sample description space”, “possibility space,” and “event space”등이 있다.
그리고 다음과 같은 조건을 만족해야 한다.
a. 단일 사건의 확률은 $[0,1]$에 있어야하고 모든 표본 공간의 확률은 1이다. $P(\Omega)=1$로
b. 확률 공간 $(\Omega, A, P)$에서 우리는 실제 현상을 담고 있어야 한다.(실제 현상을 모델링 할 수 있어야 한다. )

타겟 공간(Target Space)

머신러닝에서 우리는 확률 공간을 명시하는 것을 피하며 대신에 우리가 관심있는 분야의 확률을 $T$라고 나타낸다. 이 글에서 $T$는 Target Space를 의미하며, $T$의 구성요소를 상태(state)라고 부른다.

확률 변수(random variable)

확률 변수는 $\Omega \rightarrow T$를 맵핑해주는 것을 확률 변수(random variable)라고 한다. 확률 변수는 $\Omega$의 원소(결과)를 가지고 $T$의 사건의 특정 값 $X$를 반환하는 함수 $X: \Omega \rightarrow T$이다.

 

예시 2)

동전 두개를 연속적으로 던지는 예에서, 앞면의 갯수를 세는 확률 변수 $X$가 있다고 하면, 다음과 같이 세가지 값을 얻을 수 있다.
$$X(hh) = 2, X(ht) = 1, X(th) = 1, X (tt) = 0$$
그리고 이에 따른 $T$는 다음과 같이 나타낼 수 있다.
$$T =  { 1,2,3 }$$

유한한 공간 $\Omega, T$에 대하여 확률변수는 룩업 테이블(lookup table)로 쓰인다. $S \subseteq T$인 모든 사건에 대해 확률 변수 X에 대한 확률을 $P_x(S) \in [0,1]$의 원소로 맵핑시킨다. 다음은 해당 개념에 대한 예시이다.

 

 

예시 3)

가방에서 두개의 동전을 꺼내 확인하는 문제를 생각해보자. 하나의 가방에는 U.S의 동전을 $S$로 표시하고, 유럽의 동전을 $E$로 표기한다고 가정해보자. 이 때 표본 공간 $\Omega$는 총 4가지 경우 $(S,S),(S,E),(E,S),(E,E)$가 가능하다. 그리고 이 때에 $S$를 뽑을 확률을 0.3이라고 가정한다.

이때 우리가 $S$가 뽑히는 횟수에 관심을 둔다고 하면, 확률 변수 $X: \Omega \rightarrow T$를 정의하여 $S$를 반환하는 횟수를 나타낸다고 하자. 우리는 앞선 경우에서 $T =  { 1,2,3 }$임을 알 수 있으므로 룩업 테이블을 다음과 같이 표기 해줄 수 있다.

$$X((S,S))=2, X((E,S))=1, X((S,E))=1, X((E,E))=0$$

첫번째 동전과 두번째 동전은 독립적으로 시행되므로(Section 6.4.5) 각 확률변수에 대한 확률질량함수는 다음과 같이 정의된다.(Section 6.2.1)

$$P(X = 2) = P((S,S)) = P(S) · P(S) = 0.3 · 0.3 = 0.09$$

$$P(X =1)=P((S,E)∪(E,S)) = P ((S, E)) + P ((E, S))
= 0.3 · (1 − 0.3) + (1 − 0.3) · 0.3 = 0.42$$

$$P(X = 0) = P((E,E)) = P(E) · P(E)
= (1 − 0.3) · (1 − 0.3) = 0.49$$

이 연산에서 $P(X = 0) = P((E,E))$로 한 것 처럼 우리는 표본 공간(The sample space $\Omega$)의 확률과 X의 결과값을 동일시하여 계산을 했다. 두개의 동전을 연속해서 던지는$T$의 하나의 결과값 같이 $X: \Omega \rightarrow T$와 $S \subseteq T$를 만족하는 $T$에 대해서 생각해보자. $X^{−1}(S)$를 $X$의 pre-image라고 라고 가정해보면, $\Omega$의 원소는 $S$에 $X; {\omega \in \Omega : X(\omega) \in S}$를 이용해 맵핑할 수 있다. 해당 관계는 아래와 같이 나타낼 수 있다.

$$P_X(S)=P(X \in S) = P(X^-1(S)) = P( { \omega \in \Omega : X(\omega) \in S})$$

좌변을 통해 우리가 관심을 가지고 있는 확률임을 알 수 있으며, 이는 확률변수 $X$를 통해 $\Omega$에 매핑됨을 알 수 있다. 따라서 확률변수(X)는 특정한 확률분포($P_X$)에 매핑되어 있다고 볼 수 있다. 따라서 이때의 $P_X$ 는 law 또는 분포(distribution)라고 부른다.

참고3. Target Space의 종류

여기서 Target Space는 확률 변수 X를 나타내기 위해 쓰였다. T가 유한하거나 무한히 셀수 있으면 이산확률변수(discrete random variable)이라고 부르며, 셀수 없이 무한한 경우 연속확률변수(continuous random variable)이라고 부른다.

통계(Statistics)

통계(Statistics)는 종종 확률분포와 함께 소개되지만, 불확실성의 다른 측면을 다룬다. 따라서 이 둘은 어떠한 확률 통계적 문제를 접근할 때 다른 방식으로 접근한다.

확률	통계
확률로 접근한 프로세스 모델을 다루거나 확률 변수를 기반으로 하여 어떠한 일이 일어나는지 접근하여 해당 사건에 대한 확률적 규칙을 발견하는데 초점을 둔다.	이미 일어난 일에 대해 다루며, 해당 관측값에 대한 설명을 할 수 있는 프로세스에 초점을 준다.

머신러닝은 데이터에 대해 설명할 수 있는 최적화된 모델을 만든다는 측면에서 통계와 가깝다고 할 수 있다. 하지만, 여기서 확률을 사용하여 데이터에 최적화(best-fitting)된 값을 찾을 수 있도록 노력한다.

 

참고4. 머신러닝과 일반화 오류에 대한 추가자료
머신러닝의 또 다른 측면은 우리가 "일반화 오류"에 관심이 있다는 것이다.( Section.8). 만든 모델의 미래의 실제 데이터가 과거에 데이터에 대한 모델링을 통해 예측값과 다르다는 것을 의미한다. 미래예측은 확률과 통계에 기반하지만, 대부분은 내용은 이 챕터의 범위를 벗어난다. 해당 부분은 Bucheron 외(2013)와 Shalev-Shwartz 및 Ben-David(2014)의 책을 통해 공부할 수 있다. 이외의 통계에대한 추가적인 내용은 Section 8에서 다룰 예정이다

Discrete and Continuous Probabilities

확률 함수

이번 섹션에서는 섹션6.1에서 소개된 바와 같이 사건의 확률 표현 방법에 대해서 설명한다. Target Space가 이산형(Discrete)인지 혹은 연속형(Continous)인지에 따라 확률분포를 접근하는 방법이 달라진다.

확률질량함수(probability mass function)

Target Space $T$가 이산형(Descrete)할 때 확률 $x \in T$f로 특정할 수 있고 확률 변수 $X$가 $P(X = x)$로 나타낼 수 있다. 이 때 이산형 확률 변수(Descrete Random Variable) X에 대한 함수 $P(X = x)$는 확률 질량 함수(probability mass function)라고 한다.

누적분포함수(cumulative distribution function)

Target Space $T$가 연속형(Continous), 일차원 함수 처럼 확률 변수 $X$를 특정 범위내의 확률로 정의하는게 자연스럽다. 따라서, 일반적으로 확률 변수 X를 $P(a \leq X \leq b)$ (단,$a<b$)로 나타낸다. 또는 확률 변수 $X$는 $P( X \leq x)$로 표기하며 $x$ 보다 작을 확률을 의미한다. 연속 확률 변수 $X$에 대한 $P( X \leq x)$를 누적분포함수(cumulative distribution function)라고 한다.

참고1. 단일변수(Univarate), 다변수(multivarate) 확률

univariate distribution를 하나의 확률변수에 대한 분포로 사용할 것이다(state는 non-bold x로 나타낸다). 두개 이상의 확률변수에 대한 분포는 multivariate 분포로 사용할 것이며, 확률변수를 벡터를 이용한다(state는 bold x로 나타낸다)

이산 확률(Discrete Probabilities)

Target space가 이산형(Discrete)일 때 아래 그림과 같이 확률 분포를 다차원 배열을 여러개의 확률변수로 채우는 것으로 생각해볼 수 있다.

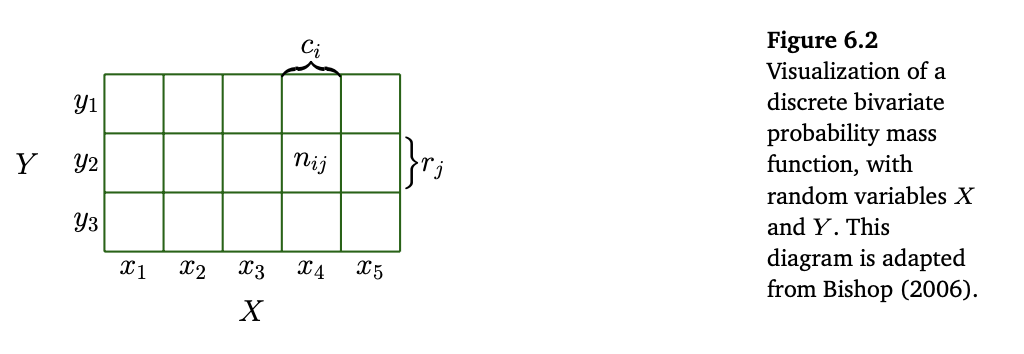
Target space의 joint probability(결합확률)는 각 확률변수의 target space에 대한 데카르트 곱(Cartesian Product)로 볼 수 있다. 이는 다음식과 같이 정의 된다.

$$P(X=x_i,Y =y_j)= \frac {n_{ij}} N$$
$n_{ij}$는 $x_i$와 $y_j$ 사건이 동시에 일어나는 경우의 수이며, $N$은 모든 경우의 수를 말한다. 따라서 결합확률은 다음과 같이 표기할 수도 있다.

$$P(X =x_i,Y =y_j)=P(X =x_i ∩Y =y_j)$$

앞서 본 그림1은 확률 밀도함수(pmf)를 시각화 한것으로, 확률변수 $X,Y$에 대해 $X=x_i, Y =y_j$에 대한 확률 값으로 $p(x,y)$로 표기 할 수 있다. 또한

1. 주변확률 분포(marginal distribution) : 확률변수 $X,Y$에 대해 서로에 무관한 값을 취하여 나타내는 확률분포를 $p(x)$라고 쓴다. $X ∼ p(x)$ 는 확률 변수 $X$가 $p(x)$에 의해 분포될 때 사용한다.
2. 조건부 확률(conditional distribution) : 한 확률 변수를 고정하고 다른 확률변수에 대한 확률을 구하는 것을 조건부 확률이라고 하며 $p(x|y)$로 표기한다.
3. 예시1)

그림 1과 같이 두개의 확률변수 $X,Y$에 대해서 $X$는 5가지 가능한 상태가 있고, $Y$는 3가지 가능한 상태가 있다고 가정하자. $n_{ij}$는 $X =x_i$,$Y =y_j$인 경우라 하고, $N$을 모든 경우에 대한 확률 변수라고 가정하자. 이 때 $c_i$를 $i$번째 행의 합 $c_i=\sum_{j=1}^3 n_{ij}$라고 하고, 이 때 $r_i$를 $i$번째 행의 합 $r_i=\sum_{i=1}^5 n_{ij}$라고 하면 확률 변수 $X,Y$에 대한 주변확률분포(marginal distribution)과 조건부 확률(Conditional Probability)를 명확하게 구할 수 있다.


주변확률분포(marginal distribution)
$$P(X=x_i)= \frac {c_i} {n_{ij}} = \frac {\sum_{j=1}^3 n_{ij}} N$$
$$P(X=x_i)= \frac {r_j} {n_{ij}} = \frac {\sum_{i=1}^5 n_{ij}} N$$


조건부 확률(Conditional Probability) : 각 행, 열을 하나의 셀(cell)로 취급하면 다음과 같이 구해줄 수 있다.

• $X$가 주어졌을 때 조건부 확률
  $$P(X =y_j | Y =x_i) = \frac {n_{ij}} {c_i}$$
• $Y$가 주어졌을 때 조건부 확률
  $$P(X =x_i | Y =y_j) = \frac {n_{ij}} {r_j}$$
• 모든 확률의 합*
  또한 각 확률변수 X에 대한 그리고 Y에 대한 확률의 합을 구해보면 다음이 성립함을 알 수 있다.
  $$\sum_{i=1}^5 P(X =x_i)=1$$
  $$\sum_{j=1}^3 P(Y =y_j)=1$$

참고2. 머신러닝과 이산확률

머신러닝에서 이산확률은 범주형 변수(categorical values)를 다룰 때 사용한다. 예를 들어 범주적 특징을 가진 대학의 학위를 이용해서 연봉을 예측 한다던지, 필기 인식을 위한 알파벳의 범주적 라벨링 같은 것들을 이용한다. 또한 이산형 변수는 유한한 연속확률분포를 결합한 모델링에도 자주 사용된다.(Section 11)

연속 확률(Continuous Probabilities)

유의사항

이 섹션에서 확률변수는 실제 값(real-valued)을 고려한다. 따라서 Target Space는 실수 $\rm I!R$에 안에 있는 선형구간에서 고려한다. 연속 확률 변수를 유한한 크기의 이산 확률 공간을 가진 것처럼 연산을 할 수 있다고 가정한다. 그러나 이러한 가정은 다음 두 가지 상황에서는 정확하지 않는다.

1. 어떤 실험을 무한히 자주 반복하는 경우
   • 기계 학습에서 일반화 오류를 논의할 때 발생한다(Section 8)
2. $\rm I!R$의 구간내에서 점을 점으로 표현하고 싶은 경우
   • 두번째 상황은 가우스와 같은 연속 확률분포에 대해 논의할 때 발생.(Section 6.5)

직관적인 이해을 돕기 위해, 정확성이 부족하더라도 해당 개념에 대해 간단한 소개를 진행하였다. 따라서 유의하여 읽어주길 바란다.

참고3. 연속확률과 비선형적인 기술

연속확률 공간에서필요한 두가지 비선형적인 기술이 있다.

1.사건 공간을 정의하는데 사용되었던 모든 부분 집합은 잘 작동하지 않는다.사건 공간은 여집합, 교집합, 합집합에 대해 잘 동작하도록 제한될 필요가 있다

2.이산확률의 원소들을 세는 작업으로 만들었던 연속확률 공간의 확률을 다루기 어렵다는 사실이다.해당 공간(집합)의 크기를 측정값(measure)이라고 부른다. 예를 들어 이산집합의 구간, 부피 모두 측정값(measures)으로 부른다. 집합 연산이 잘 작동하며 체계성을 갖춘 집합을 Borel σ-algebra라고 부른다.

Betancourt는 기술적 문제에 얽매이지 않고 집합론으로 확률 공간의 구성을 자세히 설명한다.(https://tinyurl.com/yb3t6mfd). 정확한 확률공간의 정의는 Billingsley (1995) and Jacod and Protter (2004)을 참고하면 된다

연속확률 공간의 정의

이 확률 공간에서 실제 값(real-valued)를 가진 확률변수들은 Borel σ-algebra를 따른다. 또한 $\mathbb{R}^D$의 확률 변수들은 확률 변수 벡터로 간주한다.

확률 밀도 함수(Probability Density Function)

정의 1 : 확률밀도함수(Probability Density Function)

• 함수 $f : \mathbb{R}^D \rightarrow \mathbb{R}$는 확률밀도함수(Probability Density Function)라고 부르며, $pdf$라고 부른다. 그리고 다음을 만족한다.

1. $\forall x\in \mathbb{R}^D$
2. 적분을 가능해야하며 아래 식을 만족한다.
   $$\int_{\mathbb{R}^D} f(x)dx=1$$

참고4. 이산확률 변수와 확률 질량함수

이산확률 변수의 확률 질량 함수(pmf)인 경우 적분(intergra)이 합(summation)으로 대체 된다.

모든 확률 밀도 함수의 적분 값은 음의 값을 가질 수 없으며 1이다. 아래의 식 $a,b \in \mathbb{R}$이고 $x \in \mathbb{R}$이고 연속 확률 변수의 결과값은 다음과 같은 식으로 표현한다.

$$P(a \leq X \leq b) = \int_a^b f(x)dx$$

States $x \in \mathbb{R}^D$도 $x \in \mathbb{R}$도 유사하게 정의된다. 그리고 이러한 관계를 law 또는 분산(distribution)이라고 부른다.

참고5. 연속 확률 변수와 확률 질량 함수

이산 확률 변수와 다르게 연속 확률 변수 X가 특정 값 x에서의 확률P(X = x)는 0이다. 이는 해당 적분 구간의 범위를 a = b와 같게 하기 때문이다.

누적 분포 함수(Cumulative Distribution Function)

정의 1 : 누적 분포 함수(Cumulative Distribution Function)
$x \in \mathbb{R}^D$를 만족하는 multi-variate 확률 변수 $X$의 누적 분포 함수(cdf)는 다음과 같다.


$$F_X(x) = P(X_1 \leq x_1,...,X_D \leq x_D)$$


위 식은 $X = [X_1,...,X_D]^⊤, x = [x_1,...,x_D]^⊤$를 만족하며, 우변은 확률 변수 $X_i$가 $x_i$보다 작거나 같은 경우의 확률을 의미한다.

누적분포 함수(cdf)는 다음과 같은 확률 밀도 함수(the probability density function)의 적분으로도 표현할 수 있다.

$$F_X(x) =\int_{-\infin}^{x_i} ...\int_{-\infin}^{x_D} f(z_1, ..., z_d)dz_1...dz_d$$

참고6. 유의사항

1.두가지 구별된 다른 확률분포를 공부하고 있다는 걸 명심해야한다. 첫 번째로 확인한 건 f(x)로 명시된 pdf는 양의 함수이고, 적분하면 1이되야 된다는 것이다. 두번째는 확률 변수 X와 pdf f(x)의 관계이며, 확률 변수 X에 대한 law라는 것이다.

2.pdf가 없는 cdf가 있다는 사실도 유의해야 한다.

이 책에서는 $f(x)$와 $F_X(x)$를 구분해서 사용하지 않는다. 그 이유는 pdf와 cdf를 대개의 경우 구분하지 않기 때문이다 .하지만 Section 6.7에서는 해당 개념에 대해서 구분해서 생각해야 할 것이다.

이산 확률 분포와 연속 확률 분포의 구분(Contrasting Discrete and Continous Distributions)

앞에서 언급하였듯이 확률은 양수이며 모든 가능한 확률의 합은 1이다.(Section 6.1.2). 이산 확률 변수에서 확률은 구간 [0,1]사이에 있어야 한다. 연속 확률 변수에서 확률 변수의 값은 1보다 클수도 있다. 해당 내용을 이산 균등 분포, 연속 균등 분포 그림에서 확인할 수 있다.

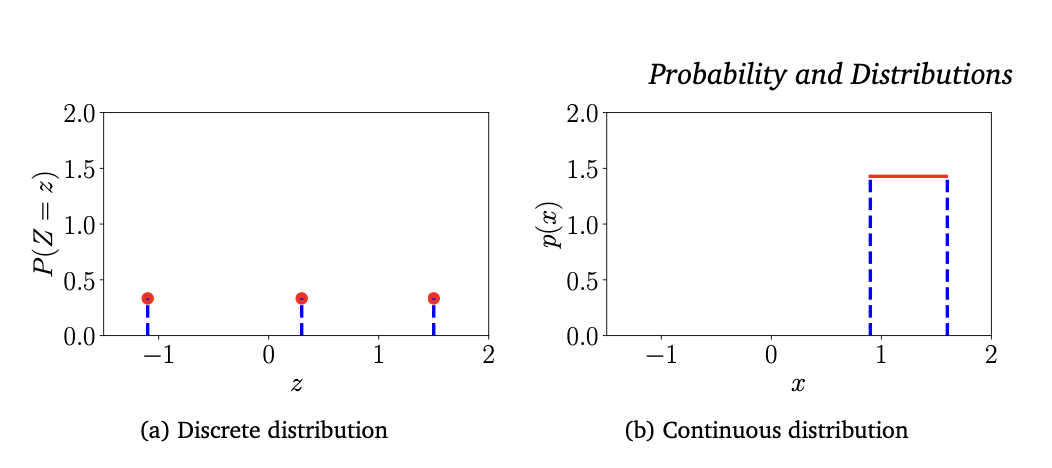
예시 1
이 예시에서는 모든 확률이 동일하게 일어나는 균등분포를 가정한다. 그리고 이 균등분포에서 이산/연속 확률 변수의 차이점을 살펴보자
$Z$를 이산 균등 분포의 확률변수라고 가정하자. 해당 값은 아래와 같이 ${z = −1.1, z = 0.3, z = 1.5}$를 가진다. 그렇다면 이 확률변수의 확률 질량 함수는 아래와 같다.

또는 이 함수를 그림2에서의 확률 변수를 $x$축으로 하고 확률을 $y$축으로 하는 (a)그래프라고 생각해줄 수 있다. 이처럼 연속 확률 변수에 대한 그래프는 확률 변수를 $x$축으로 하고 확률을 $y$축으로 하는 (b)그래프라고 생각해줄 수 있다. 그래프를 통해 $0.9\leq X \leq 1.6$ 구간의 확률 값은 1보다 클 수 있음을 알 수 있지만, 적분 값은 최대 1이 넘지 않는다.


$$\int_{0.9}^{1.6} f(x)dx=1$$

참고7. 유의사항

1.이산 확률 분포에 유의점이 있다. Z의 값들은 어떤 구조도 갖지 않는다. 구분지어줄 수 없다는 것인데, 머신러닝에서는 예시와 같이 값이 부여되어 대소가 생겨 비교할 수 있게 된다. 그리고 이러한 숫자 값을 지정하게 되면, 이산변수의 값은 확률의 기댓값을 고려할 수 있게 되어 유리한 측면디 있다.

2.부정확하더라도 '확률분포'(descrete distribution)이라는 표현을 이산 확률 변수의 pmf뿐만이 아니라 연속확률 변수의 pdf를 나타내는데도 책에서는 활용된다. 따라서 맥락을 통해 해당 개념을 확인해야한다.

머신러닝에서 표본공간 $\Omega$, 사건 공간 $T$, 확률 변수를 구분해서 표기하지 않는다. 확률 변수 $X$가 가능한 모든 결과 값은 $x \in T , p(x)$로 임의의 확률 변수 $X$가 가질 변수를 의미합니다. 이산 확률 변수의 경우 이를 확률 질량 함수라고 하는 $P(X = x)$로 쓴다. 이산확률 변수의 확률 질량 함수(pmf)와 연속 확률 변수의 확률 밀도 함수(pdf)는, 또한 더 나아가 누적 분포 함수(cdf)도 확률(distribution)라고 대신 쓸 것이다.

또한 $X$를 단일/다변수 확률 변수를 표기할 것이며, 해당 부분에 대해서 정리한 것은 아래의 표와 같다.

타입(Type)	점 확률(point probability)	구간 확률(Interval Probability)
이산(Discrete)	$P(X=x)$ 확률질량함수(pmf)	해당 사항 없음
연속(Continuous)	$p(x)$확률밀도함수(pdf)	$P(X \leq x)$ 누적분포함수(cdf)

Sum Rule, Product Rule, and Bayes’ Theorem

배경

확률 이론는 논리적 추론의 확장으로 생각할 수 있다. 이 책의 확률의 규칙은 데이터를 충족함으로써 설계 된다.(Jaynes, 2003, 2장, Section 6.1). 확률론적 모델링(Section 8.4)은 머신러닝의 학습 방법의 원칙 및 기초를 제공한다. 일단 문제 설정 및 데이터의 불확실성에대한 확률 분포(Scection 6.2)를 정의하면, Sum Rule과 Product Rule이라는 두가지 규칙이 있는 것을 확인할 수 있다.

$p(x, y)$는 확률 변수 x, y의 결합분포이다. 확률분포 $p(x)$와 $p(y)$는 대응하는 주변 분포이고, $p(y|x)$는 x가 일어났을 때 y의 조건부 확률이다. 주변 분포, 조건부 확률, 그리고 확률 분포를 이용하면 Sum Rule과 Product Rule을 도출 할 수 있다.(Section 6.2)

Sum 규칙(Sum Rule)

Sum 규칙(Sum Rule)은 아래와 같이 표현할 수 있다. (확률 변수 $Y$의 Target Space의 원소 $\mathcal{Y}$와 매핑된다.)

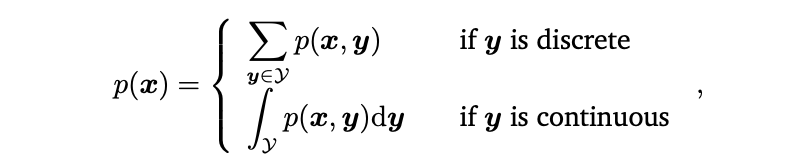
이 식이 의미하는 것은 모든 확률 변수 $Y$의 모든 값 $y$에 대한 합계 혹은 적분 값을 의미한다. 이러한 Sum Rule는 marginalization property 라고 알려져있다. Sum Rule은 또한 주변 확률과 결합 확률을 연관 시킨다. 일반적으로 결합확률은 두 개 이상의 확률 변수를 가지고 있을 때, Sum Rule은 확률 분포의 하위 집합에 적용할 수 있어, 잠재적으로 하나 이상의 확률 변수는 주변 분포를 가지게 된다.

보다 구체적으로, 만약 $x = [x_1 , . . . , x_D ]^T$ 이면 $x_i$를 제외한 모든 확률 변수를 더하거나 적분함으로써 이외의 값은 marginalization property를 갖게된다.

$$p(x_i) =\int_{p(x_1, ..., x_D)}dx_{\i}$$

(\i 는 i만 제외하고 라는 의미로 쓰인다.)

참고1. Sum Rule과 컴퓨터 계산량 문제

확률론적 모델링의 컴퓨터 계산량 문제는 Sum Rule을 적용하면서 발생한다. 많은 양의 이산 확률 변수가 있을 경우, Sum Rule은 고차원의 합 혹은 적분을 하게 된다. 이러한 고차원의 합/적분은 컴퓨터 연산을 어렵게 하며, 얼마나 걸리는지 적당한 시간을 알기 힘들다.

Product 규칙(Product Rule)

두 번째 규칙은 Product Rule으로 다음 식을 이용하여 결합 확률을 조건부 확률과 연관시킨다.

$$p(x, y) = p(y | x)p(x)$$

Product 규칙에서 모든 결합 분포에 있는 두개의 다른 확률 변수는 확률 곱으로 인수분해가 될 수 있음을 알 수 있다. 두 인수는 각각 주변 확률 분포 $p(x)$와 x가 일어날 확률에 대한 y가 일어날 확률인 조건부 확률 $p(y|x)$가 된다. 임의의 $p(x, y)$를 나타내기에
$p(x, y) = p(x | y)p(y)$로도 표현 할 수 있다. 해당 확률은 이산 확률 변수에서는 확률 질량 함수(pmf), 연속 확률 변수에서는 확률 밀도 함수(pdf)로 표현된다.

베이즈 정리(Bayes’ theorem)

머신러닝과 베이즈 통계(Bayesian statistics)에서, 우리는 관측되지 않거나 주어지지 않은 확률 변수의 확률 값을 구해야하는 경우가 있다. 관측되지 않은 확률변수 $x$에 대한 사전 지식 사전 지식 $p(x)$와 $x$와 확률 변수 $y$ 의 조건부 확률 $p(y | x)$를 가지고 있다고 가정하자. 만약 y를 관찰수 있으면 우리는 베이즈 정리(Baye's therorem)을 사용하여 y에 대한 $x$의 어떤 결론(사후 확률, $p(x|y)$)를 구할 수 있다.

베이즈 정리 Bayes’ theorem (Bayes’ rule or Bayes’ law)

$$p(x, y) = p(x | y)p(y)= p(y | x)p(x)$$

$$p(x|y)p(y) = p(y|x)p(x)\Leftrightarrow p(x|y) = \frac{p(y | x)p(x)}{p(y)}$$

사전 확률(prior)

$p(x)$는 사전 확률을 의미하며, 어떠한 데이터도 관찰 되지 않은 시점에서 가지고 있는 주관적인 사전 지식이다. 상황에 맞는 사전 확률을 선택해야 하며, 0이 아닌 확률 질량/밀도 함수 값을 가지고 있어야 한다.

우도 (likelyhood)

$p(y|x)$는 x,y의 연관성을 나타내고 이산확률분포의 경우 $x$가 주어졌을 때 $y$에 대한 확률이된다. 중요한 것은 $x$의 분포가 아니라 $y$의 확률 분포를 보여준다는 것이다. $y$에대한 x의 우도", $x$에 대한 y의 확률이라고 한다.

사후 확률(Posterior)

$p(x|y)$은 사후 확률을 의미하며, 베이지안 통계에서 quantity of interest라고 하며, 궁극적으로 구하려는 값이다. $y$가 일어났을 때 $x$의 확률을 의미한다.

marginal likelihood/evidence

$$p(y):= \int p(y|x)p(x) dx \mathbb{E}(X)$$

위 식을 marginal likelihood/evidence라고 부른다. 우변은 평균을 의미한다.(Section 6.4.1)

정의에 의해, marginal likelihood는 (6.23)의 분자를 잠재변수
$x$에 대해 적분한다. 그러므로 marginal likelihood는
$x$에 대해 독립이며, 사후확률 $p(x|y)$가 정규화가된다. 또한, 이는 사전 확률 $p(x)$에 대한 우도 기대값(expected likelihood)로 해석할 수 있다. 사후 확률의 정규화는 Section 8.6에서 배울 베이지안 모델함수에서 중요한 요인이 된다.

참고1. 베이지안(Bayesian Statistics)

베이즈 통계학에서 사후분포는 quantity of interest로, 데이터와 사전확률로부터 가능한 모든 정보를 담고 있다. 사후확률을 따르는 대신, 사후확률의 최대값과 같은 통계량에 관심을 갖는 것도 가능하다. 그러나 이는 정보의 손실을 야기한다. 더 큰 맥락을 생각해보면, 사후확률은 의사결정 시스템에서 사용할 수 있으며, 완전 사후확률을 갖는 것은 매우 유용하며 robust한 결정을 내릴 수 있게된다.

예를 들어 강화학습에서 Deisenroth et al. 2015는 plausible transition functions의 완전 사후확률분포가 매우 빠른 학습(data/sample efficient)을 가능케 했으며, 사후 확률의 최댓값을 이용하는 방법은 일관되게 안 좋은 결론을 도출하였다. 따라서 완전 사후확률분포는 downstream task에서 매우 유용하다고 할 수 있다. 이는 Chapter 9의 선형 회귀의 관점에서 다시 살펴보도록 하겠다.

배경

확률 이론는 논리적 추론의 확장으로 생각할 수 있다. 이 책의 확률의 규칙은 데이터를 충족함으로써 설계 된다.(Jaynes, 2003, 2장, Section 6.1). 확률론적 모델링(Section 8.4)은 머신러닝의 학습 방법의 원칙 및 기초를 제공한다. 일단 문제 설정 및 데이터의 불확실성에대한 확률 분포(Scection 6.2)를 정의하면, Sum Rule과 Product Rule이라는 두가지 규칙이 있는 것을 확인할 수 있다.

$p(x, y)$는 확률 변수 x, y의 결합분포이다. 확률분포 $p(x)$와 $p(y)$는 대응하는 주변 분포이고, $p(y|x)$는 x가 일어났을 때 y의 조건부 확률이다. 주변 분포, 조건부 확률, 그리고 확률 분포를 이용하면 Sum Rule과 Product Rule을 도출 할 수 있다.(Section 6.2)

Sum 규칙(Sum Rule)

Sum 규칙(Sum Rule)은 아래와 같이 표현할 수 있다. (확률 변수 $Y$의 Target Space의 원소 $\mathcal{Y}$와 매핑된다.)

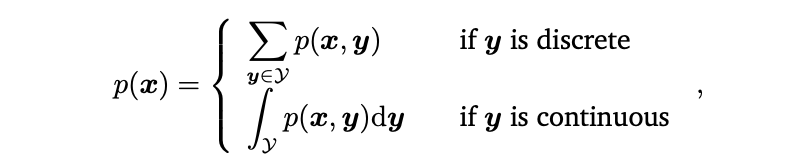
이 식이 의미하는 것은 모든 확률 변수 $Y$의 모든 값 $y$에 대한 합계 혹은 적분 값을 의미한다. 이러한 Sum Rule는 marginalization property 라고 알려져있다. Sum Rule은 또한 주변 확률과 결합 확률을 연관 시킨다. 일반적으로 결합확률은 두 개 이상의 확률 변수를 가지고 있을 때, Sum Rule은 확률 분포의 하위 집합에 적용할 수 있어, 잠재적으로 하나 이상의 확률 변수는 주변 분포를 가지게 된다.

보다 구체적으로, 만약 $x = [x_1 , . . . , x_D ]^T$ 이면 $x_i$를 제외한 모든 확률 변수를 더하거나 적분함으로써 이외의 값은 marginalization property를 갖게된다.

$$p(x_i) =\int_{p(x_1, ..., x_D)}dx_{\i}$$

(\i 는 i만 제외하고 라는 의미로 쓰인다.)

참고1. Sum Rule과 컴퓨터 계산량 문제

확률론적 모델링의 컴퓨터 계산량 문제는 Sum Rule을 적용하면서 발생한다. 많은 양의 이산 확률 변수가 있을 경우, Sum Rule은 고차원의 합 혹은 적분을 하게 된다. 이러한 고차원의 합/적분은 컴퓨터 연산을 어렵게 하며, 얼마나 걸리는지 적당한 시간을 알기 힘들다.

Product 규칙(Product Rule)

두 번째 규칙은 Product Rule으로 다음 식을 이용하여 결합 확률을 조건부 확률과 연관시킨다.

$$p(x, y) = p(y | x)p(x)$$

Product 규칙에서 모든 결합 분포에 있는 두개의 다른 확률 변수는 확률 곱으로 인수분해가 될 수 있음을 알 수 있다. 두 인수는 각각 주변 확률 분포 $p(x)$와 x가 일어날 확률에 대한 y가 일어날 확률인 조건부 확률 $p(y|x)$가 된다. 임의의 $p(x, y)$를 나타내기에
$p(x, y) = p(x | y)p(y)$로도 표현 할 수 있다. 해당 확률은 이산 확률 변수에서는 확률 질량 함수(pmf), 연속 확률 변수에서는 확률 밀도 함수(pdf)로 표현된다.

베이즈 정리(Bayes’ theorem)

머신러닝과 베이즈 통계(Bayesian statistics)에서, 우리는 관측되지 않거나 주어지지 않은 확률 변수의 확률 값을 구해야하는 경우가 있다. 관측되지 않은 확률변수 $x$에 대한 사전 지식 사전 지식 $p(x)$와 $x$와 확률 변수 $y$ 의 조건부 확률 $p(y | x)$를 가지고 있다고 가정하자. 만약 y를 관찰수 있으면 우리는 베이즈 정리(Baye's therorem)을 사용하여 y에 대한 $x$의 어떤 결론(사후 확률, $p(x|y)$)를 구할 수 있다.

베이즈 정리 Bayes’ theorem (Bayes’ rule or Bayes’ law)

$$p(x, y) = p(x | y)p(y)= p(y | x)p(x)$$

$$p(x|y)p(y) = p(y|x)p(x)\Leftrightarrow p(x|y) = \frac{p(y | x)p(x)}{p(y)}$$

사전 확률(prior)

$p(x)$는 사전 확률을 의미하며, 어떠한 데이터도 관찰 되지 않은 시점에서 가지고 있는 주관적인 사전 지식이다. 상황에 맞는 사전 확률을 선택해야 하며, 0이 아닌 확률 질량/밀도 함수 값을 가지고 있어야 한다.

우도 (likelyhood)

$p(y|x)$는 x,y의 연관성을 나타내고 이산확률분포의 경우 $x$가 주어졌을 때 $y$에 대한 확률이된다. 중요한 것은 $x$의 분포가 아니라 $y$의 확률 분포를 보여준다는 것이다. $y$에대한 x의 우도", $x$에 대한 y의 확률이라고 한다.

사후 확률(Posterior)

$p(x|y)$은 사후 확률을 의미하며, 베이지안 통계에서 quantity of interest라고 하며, 궁극적으로 구하려는 값이다. $y$가 일어났을 때 $x$의 확률을 의미한다.

marginal likelihood/evidence

$$p(y):= \int p(y|x)p(x) dx \mathbb{E}(X)$$

위 식을 marginal likelihood/evidence라고 부른다. 우변은 평균을 의미한다.(Section 6.4.1)

정의에 의해, marginal likelihood는 (6.23)의 분자를 잠재변수
$x$에 대해 적분한다. 그러므로 marginal likelihood는
$x$에 대해 독립이며, 사후확률 $p(x|y)$가 정규화가된다. 또한, 이는 사전 확률 $p(x)$에 대한 우도 기대값(expected likelihood)로 해석할 수 있다. 사후 확률의 정규화는 Section 8.6에서 배울 베이지안 모델함수에서 중요한 요인이 된다.

참고1. 베이지안(Bayesian Statistics)

베이즈 통계학에서 사후분포는 quantity of interest로, 데이터와 사전확률로부터 가능한 모든 정보를 담고 있다. 사후확률을 따르는 대신, 사후확률의 최대값과 같은 통계량에 관심을 갖는 것도 가능하다. 그러나 이는 정보의 손실을 야기한다. 더 큰 맥락을 생각해보면, 사후확률은 의사결정 시스템에서 사용할 수 있으며, 완전 사후확률을 갖는 것은 매우 유용하며 robust한 결정을 내릴 수 있게된다.

예를 들어 강화학습에서 Deisenroth et al. 2015는 plausible transition functions의 완전 사후확률분포가 매우 빠른 학습(data/sample efficient)을 가능케 했으며, 사후 확률의 최댓값을 이용하는 방법은 일관되게 안 좋은 결론을 도출하였다. 따라서 완전 사후확률분포는 downstream task에서 매우 유용하다고 할 수 있다. 이는 Chapter 9의 선형 회귀의 관점에서 다시 살펴보도록 하겠다.

Reference :

Mathematics for Machine Learning